树状数组

代码量和线段树相比少了好多。

树状数组所能解决的问题使用线段树均能解决。

主要用于求解快速前缀和——在O(logn)的时间内完成单点修改与区间查询（前缀和）。

树状数组理论上只能完成单点修改与区间查询，其他的问题均是转换为这一问题去处理。如（区间修改、单点修改 | 区间修改、区间查询）。

括号的内容太复杂了，y总说蓝桥杯不考…

​ --2022-3-31 17:28

1.存储组织

树状数组与原数组的关系可以用下图表示(图片来自博客)：

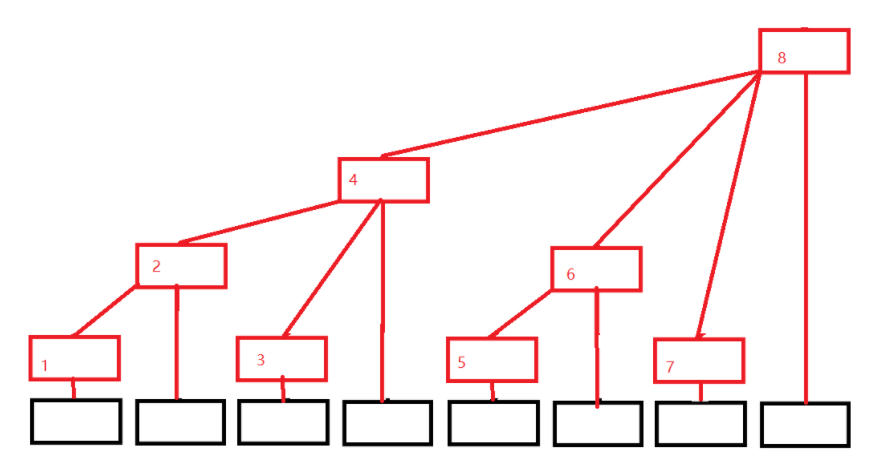
黑色数组代表原数组(a)。红色结构则代表树状数组©，存储的值是其全部子结点的值之和。可以看出:

c[1] = a[1]

c[2] = a[1] + a[2]

c[3] = a[3]

c[4] = a[1] + a[2] + a[3] + a[4]

…

c[8] = a[1] + a[2] + … + a[8]

我们定义$k$为索引$i$二进制表示中末尾连续0的个数。那么$c[i]$表示区间$(a[i - 2^k], a[i]]$的所有元素和。

2.k的求解

为了建立树状数组，我们首先要求解出$2^k$。这里利用了负数在计算机中的存储特性来求解。

负数在计算机中以补码存储。对于运算$x \& (-x)$：

• 当$x=0$时，$0 \& 0$结果仍为0.
• 当$x$为奇数时，最后一位二进制数为1，取反加1后最后一位仍然为1，因此$x$与$-x$除最后一位相同外，其余位均相反，即$x \& (-x) = 1$。正好满足了$2^0 = 1$.
• 当$x$为偶数时，且为$2$的$m$次方时，此时$x$最后有$m$位0，当$x$取反加一后，末尾正好有$m$位0，其余位均为1，因此$x \& (-x) = x$
• 当$x$为偶数，且不为2的$m$次方时，可以将$x$表示为一个奇数左移$k$位，即$x = y × (2 ^ k)$。即$x$的二进制表示下，最右边有连续$k$个0，第$k+1$位为1。取反加一后，最右侧仍为$k$个0， 第$k+1$位为1，其余位均与原数不同，因此$x \& (-x) = 2^k$。

故，$x \& (-x)$可以求得$2^k$的值。

3.索引关系

为了应付蓝桥杯，这里选择记住，特别是第二点：

• 树状数组索引从1开始。
• 索引为$x$的节点，其父节点索引为$x + lowbit(x) = x + (x \& (-x))$。

4.相关代码

我们使用$a$数组表示原数组，使用$tree$数组表示树状数组（索引从1至$n$）

4.1建树

我们将树状数组初始化为全0，那么建树的过程可以看作是为全零数组的每一个位置加上$a[i]$的过程。

for(int i = 1; i <= n; i++) add(i, a[i]);

4.2lowbit

static int lowbit(int x){
    return x & (-x);
}

4.3查询$query$

$query(x)$是要求出区间$[1, x]$的和。由于$tree[x]$存储了$a[x - lowbit(x) + 1]、a[x - lowbit(x) + 2]、...、a[x]$的和，因此只要将$x$更新为$x - lowbit(x)$，并重新执行$query(x - lowbit(x))$，如此递归直至$x = 0$即可。

static int query(int x){
    int sum = 0;
    for(int i = x; i > 0; i = i - lowbit(i)){
        sum += tree[i];
    }
    return sum;
}

4.4修改$add$

$add(x, y)$是将$a[x]$的值加上$y$。在3.索引关系中提到，$x$的父节点索引为$x + lowbit(x)$，因此通过不断的将$x$更新为$x + lowbit(x)$，即可修改全部包含$x$项的节点信息。

static void add(int x, int y){
    for(int i = x; i <= n; i = i + lowbit(i)) tree[i] += y;
}